I bring up two recurring topics...
Fresh every time around:
Question: I have a problem with the unique id for Document.ProjectInformation.
If I create two Revit project files from the same Revit template file, the project information unique ids are identical.
How can I get the different unique ids for different project files, even when they are created from the same template?
Answer: As far as I know you cannot.
I am not aware of any way to change an existing unique id.
Furthermore, even if you could change it, how are you going to guarantee that an end user does not copy an existing project file later on to reuse in another different project, thus again duplicating the existing unique id?
Therefore, I would suggest that you create your own personal project identifier that you can control as you yourself see fit, in a way that perfectly matches your own requirements.
I implemented such a system for The Building Coder
using named GUID storage for project identification.
I am not saying that my solution is perfect.
Furthermore, it is completely untested, as far as I know.
If anyone has made using of this or enhanced it in any way, please let us know.
Thank you!
An interesting discussion ensued in
the Revit API discussion forum thread on
a problem with the function Curve.Intersect(Curve):
Question:
I have a problem when I use this function with 2 lines intersecting each other in the case where they are parallel:
XYZ pt1 = new XYZ(); XYZ pt2 = new XYZ( 1, 0, 0 ); XYZ pt3 = new XYZ( -1, 0, 0 ); SetComparisonResult scr = Line.CreateBound( pt1, pt2 ) .Intersect( Line.CreateBound( pt1, pt3 ), out IntersectionResultArray ira ); if( scr == SetComparisonResult.Overlap ) monMessage += "\n Case 1 overlap" + DonneXYZ( ira.get_Item( 0 ).XYZPoint ); if( scr == SetComparisonResult.Disjoint ) monMessage += "\n Case 1 disjoint"; if( scr != SetComparisonResult.Overlap && scr != SetComparisonResult.Disjoint ) monMessage += "\n Case 1 problem";
This returns the Case 1, which is a problem (not overlap, not disjoint).
If the 2 lines are not parallel to each other, the result is overlap (correct):
XYZ pt4 = new XYZ( 0, 1, 0 ); SetComparisonResult scr2 = Line.CreateBound( pt1, pt2 ) .Intersect( Line.CreateBound( pt1, pt4 ), out IntersectionResultArray ira2 ); if( scr2 == SetComparisonResult.Overlap ) monMessage += "\n Case 2 overlap" + DonneXYZ( ira2.get_Item( 0 ).XYZPoint ); if( scr2 == SetComparisonResult.Disjoint ) monMessage += "\n Case 2 disjoint"; if( scr2 != SetComparisonResult.Overlap && scr != SetComparisonResult.Disjoint ) monMessage += "\n Case 2 problem";
I also tried to get a curve with tangent parallel with the other curve:
Arc myArc = Arc.Create( new XYZ( 0, 1, 0 ), 1.0, -0.5 * Math.PI, 0.0, XYZ.BasisX, XYZ.BasisY ); SetComparisonResult scr3 = myArc.Intersect( Line.CreateBound( pt1, pt3 ), out IntersectionResultArray ira3 ); if( scr3 == SetComparisonResult.Overlap ) monMessage += "\n Case 2 overlap " + DonneXYZ( ira3.get_Item( 0 ).XYZPoint ); if( scr3 == SetComparisonResult.Disjoint ) monMessage += "\n Case 2 disjoint"; if( scr3 != SetComparisonResult.Overlap && scr != SetComparisonResult.Disjoint ) monMessage += "\n Case 2 problem";
This result is also correct (overlap).
So, it appears that the only incorrect result is when you have 2 parallel lines.
This causes problems in my code (unexpected errors that I have to deal with) so if this could be fixed if would be great!
Answer: You say that you have a problem with the intersection of two parallel lines?
Point P = (-1,0,0) Point O = (0,0,0) Point Q = (0,0,+1) Line A from P to O Line B from O to Q
These two lines have one single common point in (0,0,0).
Whether that is to be considered an intersection depends completely on your point of view.
If the lines are considered as closed sets of points in space, they intersect in one point.
If they are considered as open sets in space, they do not intersect.
Both of these way of looking at geometrical elements are completely valid.
Mathematically speaking, you can consider this equivalent question:
Do the two intervals [-1,0] and [0,1] intersect?
These cases can only be distinguished precisely using exact arithmetic, aka arbitrary precision arithmetic.
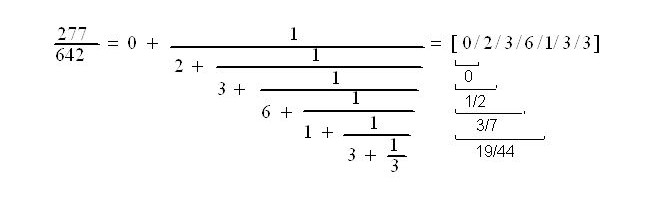
The Revit API, just like most other current geometrical programming environments, does not specify which paradigm is considered valid.
In fact, it cannot, because it does not work with exact arithmetic.
As long as we are working with imprecise double precision floating point numbers, these two cases cannot be distinguished.
The line A is considered totally equivalent to the line
Line A' from P to (-0.000000000000000000001,0,0)
What result would you consider correct for that case?
Remember, lines A and A' must be considered completely identical in all respects!
The only way I see for you to handle your problem properly using inexact floating point arithmetic is to perform a fuzzy comparison of the edge cases such as these.
I would say that this is not a bug, and there is no way to decide whether parallel lines that meet in one single point intersect or not.
Any such attempt would be completely pointless :-)
Your software needs to be implemented in a way that takes this possibility into account.
Exact comparison would be required to answer this precisely.
This is definitely not possible using floating point arithmetic.
Response: Your explanation is interesting.
Still, the bottom of the problem remains:
The way this is coded in Revit makes the results of very similar intersection problems inconsistent.
This problem arises only for Line which are parallel, not for the other types of Curves.
As I explained, this causes unexpected errors which should be avoided and can be difficult to find.
So, I believe the Curve.Intersect method should be updated on this particular point.
Except if there is a better argument not to do so...
Answer: As you can tell, I find the topic interesting and really want to help find a satisfactory solution.
If this only applies to parallel lines, I would suggest solving it for that case, because it is not hard to do.
I added IsParallel and IsCollinear predicates to The Building Coder samples for this:
public static bool IsParallel( XYZ p, XYZ q ) { return p.CrossProduct( q ).IsZeroLength(); } public static bool IsCollinear( Line a, Line b ) { XYZ v = a.Direction; XYZ w = b.Origin - a.Origin; return IsParallel( v, b.Direction ) && IsParallel( v, w ); }
The next step would be to check for the overlap including the required fuzziness in case lines are collinear.
I also discussed this with the development team, and they say:
I believe the documentation covers this case and the return is SetComparisonResult.Subset:
The inputs are parallel lines with only one common intersection point, or the curve used to invoke the intersection check is a line entirely within the unbound line passed as argument curve. If the former, the output argument has the details of the intersection point.
The customer didn't indicate what the return value was for them; if it is subset, that matches what we have told them it would be.
Response: Indeed, using SetcomparisonResult.Subset works for my problem and is much more elegant than my previous workaround solution (which was, in essence: check if SetComparisonResult is either Overlap or Disjoint; if not, check if the 2 elements are line, collinear, and have same end; if so, treat the case as Overlap).
The improved test is now:
if( scr != SetComparisonResult.Overlap && scr != SetComparisonResult.Disjoint && !( scr == SetComparisonResult.Subset && ira.Size == 1 ) )