Today I happily present a brilliant piece of Revit API news on the documentation side of things, and another handy utility method for your Revit API programming toolbox:
The contents of the Revit API help file RevitAPI.chm are finally available online.
And not only that, but the web site includes all three versions for Revit 2015, Revit 2016 and Revit 2017.
As you know, the two main pieces of Revit API documentation are the Revit API help file RevitAPI.chm, included with the Revit SDK, available from the Revit Developer Centre, and the developer guide, provided in the 'Developers' section of the online Revit Help.
The help file was not available online, though, which also means that it was not included in standard Internet searches using Google or DuckDuckGo.
With the notable exception of Revit 2014, revitapisearch.com, implemented by Peter Boyer of the Dynamo team.
Just a few weeks ago, Arif Hanif expressed interest to do the same for Revit 2017 in a couple of comments on What's New in the Revit 2017 API.
Well, someone beat him to it.
In his Revit API discussion forum thread on Revit API Documentation Online , @gtalarico says:
Since Google doesn't seem too excited to index my 60k+ page website, I wanted to share it here so people can find it and hopefully use it! : )
It currently includes the full official documentation (from the CHM file) for APIS 2015, 2016, and 2017:
It was a lot of planning and work, but came together faster and better than I expected.
Please let him know if you have any feedback on it.
Ever so many thanks to gtalarico for all his work and making this useful resource available to the global Revit API community!
Gtalarico added some additional info on the project:
The code is on github at github.com/gtalarico/revitapidocs.
The project is definately open to collaborators. Welcome!
It needs +code docs, +test coverage, and can probably be improved and optimized significantly by more seasoned web developers.
Regarding github pages, it could probably be done, but I haven't used it myself, so I don't know the limitations.
Here are some of the challenges and constraints:
XYZYesterday, I mentioned the convex hull calculation as one option for determining the bounding box of selected elements or entire model.
Maxence replied in a comment on that post and provided a convex hull implementation in C#.
It is a 2D algorithm implementing the Jarvis march or Gift wrapping algorithm:
It makes use of an extension method MinBy on the generic IEnumerable class,
from MoreLINQ by
Jonathan Skeet:
public static class IEnumerableExtensions { public static tsource MinBy<tsource, tkey>( this IEnumerable<tsource> source, Func<tsource, tkey> selector ) { return source.MinBy( selector, Comparer<tkey>.Default ); } public static tsource MinBy<tsource, tkey>( this IEnumerable<tsource> source, Func<tsource, tkey> selector, IComparer<tkey> comparer ) { if( source == null ) throw new ArgumentNullException( nameof( source ) ); if( selector == null ) throw new ArgumentNullException( nameof( selector ) ); if( comparer == null ) throw new ArgumentNullException( nameof( comparer ) ); using( IEnumerator<tsource> sourceIterator = source.GetEnumerator() ) { if( !sourceIterator.MoveNext() ) throw new InvalidOperationException( "Sequence was empty" ); tsource min = sourceIterator.Current; tkey minKey = selector( min ); while( sourceIterator.MoveNext() ) { tsource candidate = sourceIterator.Current; tkey candidateProjected = selector( candidate ); if( comparer.Compare( candidateProjected, minKey ) < 0 ) { min = candidate; minKey = candidateProjected; } } return min; } } }
With that helper method in hand, the convex hull implementation is quite short and sweet:
#region Convex Hull /// <summary> /// Return the convex hull of a list of points /// using the Jarvis march or Gift wrapping: /// https://en.wikipedia.org/wiki/Gift_wrapping_algorithm /// Written by Maxence. /// </summary> public static List<XYZ> ConvexHull( List<XYZ> points ) { if( points == null ) throw new ArgumentNullException( nameof( points ) ); XYZ startPoint = points.MinBy( p => p.X ); var convexHullPoints = new List<XYZ>(); XYZ walkingPoint = startPoint; XYZ refVector = XYZ.BasisY.Negate(); do { convexHullPoints.Add( walkingPoint ); XYZ wp = walkingPoint; XYZ rv = refVector; walkingPoint = points.MinBy( p => { double angle = ( p - wp ).AngleOnPlaneTo( rv, XYZ.BasisZ ); if( angle < 1e-10 ) angle = 2 * Math.PI; return angle; } ); refVector = wp - walkingPoint; } while( walkingPoint != startPoint ); convexHullPoints.Reverse(); return convexHullPoints; } #endregion // Convex Hull
For testing purposes, I make use of it like this in the CmdListAllRooms external command:
/// <summary> /// Return bounding box calculated from the room /// boundary segments. The lower left corner turns /// out to be identical with the one returned by /// the standard room bounding box. /// </summary> static List<XYZ> GetConvexHullOfRoomBoundary( IList<IList<BoundarySegment>> boundary ) { List<XYZ> pts = new List<XYZ>(); foreach( IList<BoundarySegment> loop in boundary ) { foreach( BoundarySegment seg in loop ) { Curve c = seg.GetCurve(); pts.AddRange( c.Tessellate() ); } } int n = pts.Count; pts = new List<XYZ>( pts.Distinct<XYZ>( new CmdWallTopFaces .XyzEqualityComparer( 1.0e-4 ) ) ); Debug.Print( "{0} points from tessellated room boundaries, " + "{1} points after cleaning up duplicates", n, pts.Count ); return Util.ConvexHull( pts); }
Initially, I did not include the call to Distinct, which eliminates duplicate points returned by Revit that are intended to represent the same room corner but have small offsets from each other due to limited precision, or too high precision, whichever way you look at it.
Here are the
diffs with just the pure convex hull implementation
and after adding the call to Distinct.
I tested it on the same ten rectangular rooms as yesterday and verified that their convex hulls correspond to their bounding boxes returned by Revit.
I also tested on the following squiggly room with some spline-shaped edges:
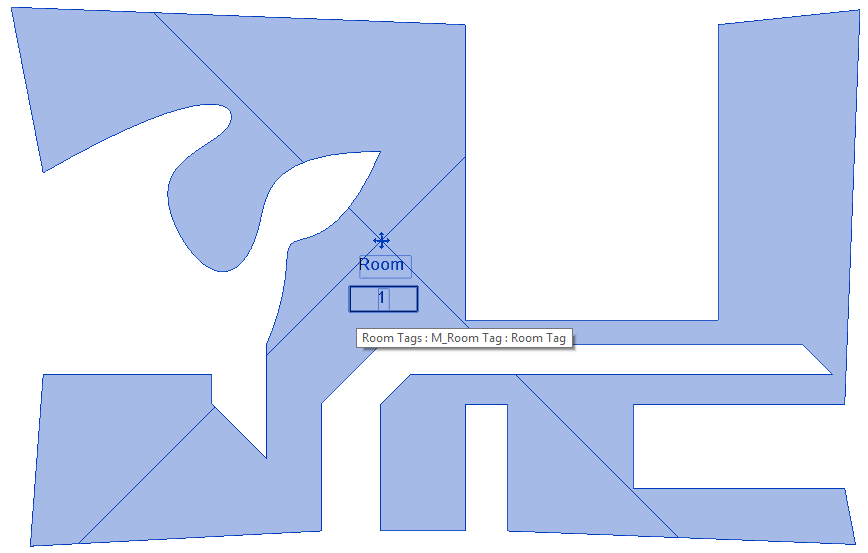
That returns the following results:
355 points from tessellated room boundaries, 324 points after cleaning up duplicates Room nr. '1' named 'Room 1' at (-77.61,15.1,0) with lower left corner (-106.43,-8.65,0), convex hull (-104.93,-8.65,0), (-40.75,-8.51,0), (-40.41,33.07,0), (-106.43,33.27,0), bounding box ((-106.43,-8.65,0),(-40.41,33.27,13.12)) and area 1483.20391607451 sqf has 1 loop and 31 segments in first loop.
Everything discussed above is published in The Building Coder samples release 2017.0.127.10.
Many thanks to Maxence for providing the nice convex hull algorithm implementation!