Here is a query and some sample code from a Revit API newbie that led to several different interesting topics, in particular some ruminations on planes, projections, picking points and common extension methods that I hope will be of use to you too – yet another Monday monster post:
Question: The macro below sets a work plane based on the active view and lets the user pick two points to get the area of a rectangle. This works for east and west elevation views, but returns an area of 0 in north and south elevation views. Any idea why this happens? If I set the work plane manually in north and south elevation views and run a version of the macro without the work plane transaction, it works fine.
Also, this macro measures along XYZ axes and won't give the correct area for, say, a wall bearing 45 degrees NE. Any ideas on how to make it more universal?
public void SetWorkPlaneAndPickPointsForArea( UIDocument uidoc ) { Document doc = uidoc.Document double differenceX; double differenceY; double differenceZ; double area; Transaction t = new Transaction( doc, "Set Work Plane" ); t.Start(); Plane plane = new Plane( doc.ActiveView.ViewDirection, doc.ActiveView.Origin ); SketchPlane sp = doc.Create.NewSketchPlane( plane ); doc.ActiveView.SketchPlane = sp; doc.ActiveView.ShowActiveWorkPlane(); t.Commit(); XYZ pt1 = uidoc.Selection.PickPoint(); XYZ pt2 = uidoc.Selection.PickPoint(); double pt1x = pt1.X; double pt1y = pt1.Y; double pt1z = pt1.Z; double pt2x = pt2.X; double pt2y = pt2.Y; double pt2z = pt2.Z; bool b; int caseSwitch = 0; if( b = ( pt1z == pt2z ) ) { caseSwitch = 1; } if( b = ( pt1y == pt2y ) ) { caseSwitch = 2; } if( b = ( pt1x == pt2x ) ) { caseSwitch = 3; } switch( caseSwitch ) { case 1: differenceX = pt2x - pt1x; differenceY = pt1y - pt2y; area = differenceX * differenceY; break; case 2: differenceX = pt2x - pt1x; differenceZ = pt1z - pt2z; area = differenceX * differenceZ; break; default: differenceY = pt2y - pt1y; differenceZ = pt1z - pt2z; area = differenceY * differenceZ; break; } area = Math.Round( area, 2 ); if( area < 0 ) { area = area * ( -1 ); } TaskDialog.Show( "Area", area.ToString() ); }
Answer: Your query and sample code lead to a whole bunch of topics and suggestions, many of which are of general interest, I hope:
I would suggest you have a look at the points you are picking and their coordinates in the debugger.
That will probably show you the problem immediately.
The simplest and safest way to handle transactions in the Revit API is to encapsulate each transaction and transaction group in a 'using' statement, which will automagically handle disposal and roll-back for you.
There is actually no need to construct a plane from the view direction and origin, and then create a sketch plane from that, because the view already has a built-in sketch plane that we can use, and that in turn has a plane defining it.
This again obviates the need for the transaction, so we can make use of this method in a read-only command as well.
You use the equality operator == to compare the floating point coordinates of the picked points.
I would recommend never doing that, because they could always be off by an infinitesimal amount, in which case the comparison would return false, even if they are almost equal, within the possible precision. You need to use fuzzy comparison for floating point numbers. Look at this discussion on real number equality testing.
That may well be the reason for the failures you mention for certain planes.
Your code could be shortened and made easier to read by using the Revit XYZ class or some other similar utility class instead of managing 3D point X, Y and Z coordinates in separate double variables.
For instance, to calculate the vector v between two given points p1 and p2, you can simply use:
v = p2 - p1;
Calculating the difference between each of the three coordinates separately and storing each of these in its own double variable would make the code several times longer and much harder to understand.
The Revit API methods prompting the user to pick a point throw an exception if the user cancels the operation.
Unfortunately and admittedly, this totally violates the rule that exceptions are and should remain exceptional.
Still, I always add a try-catch block around any pick point and other Revit API selection calls, catching the Autodesk.Revit.Exceptions.OperationCanceledException, terminating the command and returning gracefully with a result code saying Result.Cancelled or Result.Failed, as the case may be.
The main issue with the current implementation, just as you point out, is the hard-coded dependency on planes exactly aligned with the cardinal axes. The current approach will fail if the plane is angled in any way.
A better solution might be to project the two picked points onto the plane (since they are picked in the view plane, they should be located on it anyway) and determine their UV coordinates in it.
That gives you 2D points to play with, and the area calculation is trivial.
You would need something similar to the Revit API Face.Project method, which projects an XYZ point onto a face and returns an IntersectionResult object, from which the 2D UV parameters of the projected point can be determined.
Unfortunately, the Revit API does not provide a similar method for the Plane class, so we have to define it ourselves.
Alternatively, but rather a bit of an overkill, we might be able to make use the AutoCAD ARX AcGe functionality included with Revit.
It provides the Geometry.AcGe.Helper.orthoProjectIntoPlane method that does exactly what we need in this case.
Since I love geometrical calculations and all too seldom have a chance to get a nice bite of one, I added some code to The Building Coder samples to demonstrate how to implement this for you.
First, I implemented three helper .NET extension methods for the Revit API Plane class:
To quote the MSDN documentation on extension methods in the C# Programming Guide: Extension methods enable you to "add" methods to existing types without creating a new derived type, recompiling, or otherwise modifying the original type. Extension methods are a special kind of static method, but they are called as if they were instance methods on the extended type. For client code written in C# and Visual Basic, there is no apparent difference between calling an extension method and the methods that are actually defined in a type.
To implement an extension method, you create a static class with a static method taking a 'this' pointer to an instance of the class you are extending. In my case, I added a class JtPlaneExtensionMethods to The Building Coder samples Util.cs module.
Before getting into the details of implementing these methods, let's mention some basics about planes, their coordinate systems and projection onto them.
A plane can be defined by just four real numbers: three specify its normal vector, and a fourth the signed distance from the world coordinate system origin.
Revit planes are overspecified, in a way, since they define an origin plus X and Y vectors specifying the directions of the U and V coordinates of the 2D points in the plane, respectively.
A Revit plane therefore has a well-defined 2D coordinate system embedded in it.
The calculation of the distance from a point to a plane is straightforward using the dot product.
What is the dot product?
Geometrically, you can simply see it as the length of the projection of one vector onto another:
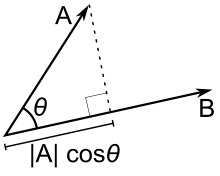
Calculating the signed distance between a 3D point and a plane in space is easy using this: determine the vector between the given point and any arbitrary point on the plane, e.g. its origin. The dot product between that vector and the plane normal is the signed distance. This assumes that the plane normal vector has unit length. The result can be either zero, negative or positive, depending on whether the given point lies on the plane or on one or the other side of it.
Here is my Revit API implementation of this; as said, it is a static method on the static JtPlaneExtensionMethods class:
/// <summary> /// Return signed distance from plane to a given point. /// </summary> public static double SignedDistanceTo( this Plane plane, XYZ p ) { Debug.Assert( Util.IsEqual( plane.Normal.GetLength(), 1 ), "expected normalised plane normal" ); XYZ v = p - plane.Origin; return plane.Normal.DotProduct( v ); }
ProjectOnto returns a 3D XYZ point representing the projection of a given point in space onto the surface of the plane. The result can be easily determined by subtracting the plane normal multiplied by the signed distance from the point:
/// <summary> /// Project given 3D XYZ point onto plane. /// </summary> public static XYZ ProjectOnto( this Plane plane, XYZ p ) { double d = plane.SignedDistanceTo( p ); //XYZ q = p + d * plane.Normal; // wrong according to Ruslan Hanza and Alexander Pekshev in their comments below XYZ q = p - d * plane.Normal; Debug.Assert( Util.IsZero( plane.SignedDistanceTo( q ) ), "expected point on plane to have zero distance to plane" ); return q; }
ProjectInto is similar to ProjectOnto but adds an important twist. Instead of a 3D XYZ point, it returns a 2D UV one representing the projection of the given point in the local coordinate system on the surface of the plane.
The 3D point calculated by ProjectOnto above is in global 3D world coordinates. The 2D point is in plane coordinates.
It can be determined by calculating the dot product of the vector between the plane origin and the projected point with the plane X and Y vectors, respectively. These two vectors determine the direction of the U and V coordinates on the plane surface:
/// <summary> /// Project given 3D XYZ point into plane, /// returning the UV coordinates of the result /// in the local 2D plane coordinate system. /// </summary> public static UV ProjectInto( this Plane plane, XYZ p ) { XYZ q = plane.ProjectOnto( p ); XYZ o = plane.Origin; XYZ d = q - o; double u = d.DotProduct( plane.XVec ); double v = d.DotProduct( plane.YVec ); return new UV( u, v ); }
Wit these helper extension methods in hand, I can reimplement your SetWorkPlaneAndPickPointsForArea method like this, renaming it to PickPointsForArea, since no workplane manipulations are required any longer to achieve the same effect:
public void PickPointsForArea( UIDocument uidoc ) { Document doc = uidoc.Document; View view = doc.ActiveView; XYZ p1, p2; try { p1 = uidoc.Selection.PickPoint( "Please pick first point for area" ); p2 = uidoc.Selection.PickPoint( "Please pick second point for area" ); } catch( Autodesk.Revit.Exceptions.OperationCanceledException ) { return; } Plane plane = view.SketchPlane.GetPlane(); UV q1 = plane.ProjectInto( p1 ); UV q2 = plane.ProjectInto( p2 ); UV d = q2 - q1; double area = d.U * d.V; area = Math.Round( area, 2 ); if( area < 0 ) { area = area * ( -1 ); } TaskDialog.Show( "Area", area.ToString() ); }
I incorporated all the code presented above in The Building Coder samples.
You can download the full solution from The Building Coder samples GitHub repository.
The version discussed above is 2015.0.111.2.
Here are direct links to the Util and CmdPickPoint3d modules, in case you prefer not to clone the whole thing.