Planar Face Transform
Here is another contribution by Joe Offord of Enclos, who already shared valuable insights on accessing curtain wall geometry, speeding up the interactive selection process, mirroring in a new family and changing the active view.
Above all, he implements all his stuff in VB, so this is also something for you VB aficionados.
This time, Joe looks at a command that redraws a planar face's edges in a drafting view. The issue is somewhat related to the discussion of polygon transformations.
However, instead of using rotations and translations, which can be difficult to determine in 3D, Joe wrote a utility function that re-maps the global coordinate system to the planar face's coordinate system using vectors and origins.
The command prompts the user to select a planar face on an elements, creates a new drafting view, retrieves the edges of the selected face, and transforms them from the 3D space to the drafting view.
To test this, I selected the following slightly lopsided wall in 3D:
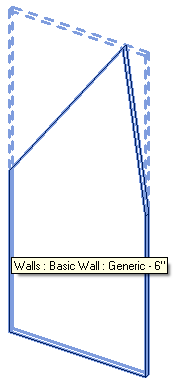
The command generated a new drafting view showing the wall profile edges like this:
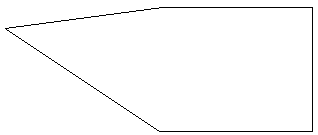
Here is the Execute method implementation for the mainline of the command:
Public Function Execute( _ ByVal commandData As ExternalCommandData, _ ByRef message As String, _ ByVal elements As ElementSet) As Result Implements IExternalCommand.Execute Dim uiapp As UIApplication = commandData.Application Dim app As Application = uiapp.Application Dim uidoc As UIDocument = uiapp.ActiveUIDocument Dim doc As Document = uidoc.Document Dim sel As Selection = uidoc.Selection Try Dim ref As Reference = sel.PickObject( _ ObjectType.Face, "Select a face") Dim elem As Element = doc.GetElement(ref) Dim gObj As GeometryObject _ = elem.GetGeometryObjectFromReference(ref) Dim face As PlanarFace = TryCast(gObj, PlanarFace) If face Is Nothing Then MsgBox("Not a planar face") End If Dim v As ViewDrafting = Nothing Dim tr As New Transaction(doc, "Draw Face") tr.Start() Try v = doc.Create.NewViewDrafting 'create a new view v.Scale = 48 '1/4" = 1'-0" 'this transform re-orients the global 'coordinate system to the face's coordinate system Dim trans As Transform _ = Util.PlanarFaceTransform(face) For Each eArr As EdgeArray In face.EdgeLoops For Each e As Edge In eArr Dim c As Curve = e.AsCurveFollowingFace(face) c = c.Transformed(trans) 'orient the curve on the XY plane doc.Create.NewDetailCurve(v, c) 'draw the curve Next Next tr.Commit() Catch ex As Exception tr.RollBack() MsgBox("Error: " + ex.Message) End Try If tr.GetStatus = TransactionStatus.Committed Then uidoc.ActiveView = v End If Catch ex As Exception MsgBox("Error: " + ex.Message) End Try Return Result.Succeeded End Function
The transformation from the planar face coordinate system is created by the following two utility methods:
''' <summary> ''' Return a transform that changes a x,y,z ''' coordinate system to a new x',y',z' system ''' </summary> Public Shared Function TransformByVectors( _ ByVal oldX As XYZ, _ ByVal oldY As XYZ, _ ByVal oldZ As XYZ, _ ByVal oldOrigin As XYZ, _ ByVal newX As XYZ, _ ByVal newY As XYZ, _ ByVal newZ As XYZ, _ ByVal newOrigin As XYZ) As Transform ' [new vector] = [transform]*[old vector] ' [3x1] = [3x4] * [4x1] ' ' [v'x] [ i*i' j*i' k*i' translationX' ] [vx] ' [v'y] = [ i*j' j*j' k*j' translationY' ] * [vy] ' [v'z] [ i*k' j*k' k*k' translationZ' ] [vz] ' [1 ] Dim t As Transform = Transform.Identity Dim xx As Double = oldX.DotProduct(newX) Dim xy As Double = oldX.DotProduct(newY) Dim xz As Double = oldX.DotProduct(newZ) Dim yx As Double = oldY.DotProduct(newX) Dim yy As Double = oldY.DotProduct(newY) Dim yz As Double = oldY.DotProduct(newZ) Dim zx As Double = oldZ.DotProduct(newX) Dim zy As Double = oldZ.DotProduct(newY) Dim zz As Double = oldZ.DotProduct(newZ) t.BasisX = New XYZ(xx, xy, xz) t.BasisY = New XYZ(yx, yy, yz) t.BasisZ = New XYZ(zx, zy, zz) ' The movement of the origin point ' in the old coordinate system Dim translation As XYZ = newOrigin - oldOrigin ' Convert the translation into coordinates ' in the new coordinate system Dim translationNewX As Double _ = xx * translation.X _ + yx * translation.Y _ + zx * translation.Z Dim translationNewY As Double _ = xy * translation.X _ + yy * translation.Y _ + zy * translation.Z Dim translationNewZ As Double _ = xz * translation.X _ + yz * translation.Y _ + zz * translation.Z t.Origin = New XYZ( _ -translationNewX, _ -translationNewY, _ -translationNewZ) Return t End Function Public Shared Function PlanarFaceTransform( _ ByVal face As PlanarFace) As Transform Return Util.TransformByVectors( _ XYZ.BasisX, _ XYZ.BasisY, _ XYZ.BasisZ, _ XYZ.Zero, _ face.Vector(0), _ face.Vector(1), _ face.Normal, _ face.Origin) End Function
Here is PlanarFaceTransform.zip including the complete source code and Visual Studio solution of this command.
Many thanks to Joe for sharing this!