Faces

This is part 5 of Scott Conover's AU 2009 class on analysing building geometry.

Faces in the Revit API can be described as mathematical functions of two input parameters 'u' and 'v', where the location of the face at any given point in XYZ space is a function of the parameters. The U and V directions are automatically determined based on the shape of the given face. Lines of constant U or V can be represented as gridlines on the face:

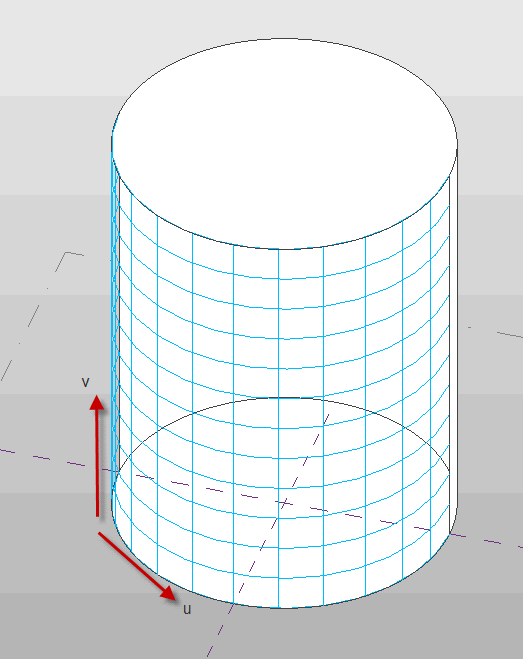
You can use the UV parameters to evaluate a variety of properties of the face at any given location:

• Whether the parameter is within the boundaries of the face, using Face.IsInside.
• The XYZ location of the given face at the specified UV parameter value. This is returned from Face.Evaluate. If you are also calling ComputeDerivatives, this is also the .Origin property of the Transform returned by that method.
• The tangent vector of the given face in the U direction. This is the BasisX property of the Transform returned by Face.ComputeDerivatives.
• The tangent vector of the given face in the V direction. This is the BasisY property of the Transform returned by Face.ComputeDerivatives.
• The normal vector of the given face. This is the BasisZ property of the Transform returned by Face.ComputeDerivatives.

All of the vectors returned are non-normalized.

Face types

Revit uses a variety of curve types to represent face geometry in a document, including the following with their corresponding Revit API representation classes:

• Plane – PlanarFace
• Cylinder – CylindricalFace
• Cone – ConicalFace
• Revolved face – RevolvedFace
• Ruled surface – RuledFace
• Hermite face – HermiteFace

Here is the definition and some notes on each of these:

• Plane: A plane defined by the origin and unit vectors in U and V.
• Cylinder: A face defined by extruding a circle along an axis. The Radius property provides the 'radius vectors' – the unit vectors of the circle multiplied by the radius value.
• Cone: A face defined by rotation of a line about an axis. The Radius property provides the 'radius vectors' – the unit vectors of the circle multiplied by the radius value.
• Revolved face: A face defined by rotation of an arbitrary curve about an axis. The Radius property provides the unit vectors of the plane of rotation, there is no 'radius' involved.
• Ruled surface: A face defined by sweeping a line between two profile curves, or one profile curve and one point. Both curve(s) and point(s) can be obtained as properties.
• Hermite face: A face defined by Hermite interpolation between points.

Mathematical representation

Mathematical representations of all of the Revit face types are given in Appendix B of Scott's handout document, and we include them here as well for easy online access. This section describes the face types encountered in Revit geometry, their properties, and their mathematical representations.

PlanarFace

A plane defined by origin and unit vectors in U and V. Its parametric equation is

CylindricalFace

A face defined by extruding a circle along an axis. The Revit API provides the following properties:

• The origin of the face.
• The axis of extrusion.
• The 'radius vectors' in X and Y. These vectors are the circle's unit vectors multiplied by the radius of the circle. Note that the unit vectors may represent either a right handed or left handed control frame.

The parametric equation for this face is:

ConicalFace

A face defined by rotation of a line about an axis. The Revit API provides the following properties:

• The origin of the face.
• The axis of the cone.
• The 'radius vectors' in X and Y. These vectors are the unit vectors multiplied by the radius of the circle formed by the revolution. Note that the unit vectors may represent either a right handed or left handed control frame.
• The half angle of the face.

The parametric equation for this face is:

RevolvedFace

A face defined by rotation of an arbitrary curve about an axis. The Revit API provides the following properties:

• The origin of the face.
• The axis of the face.
• The profile curve.
• The unit vectors for the rotated curve (incorrectly called 'Radius').

The parametric equation for this face is:

RuledFace

A ruled surface is created by sweeping a line between two profile curves or between a curve and a point. The Revit API provides the curve(s) and point(s) as properties.

If both curves are valid, the parametric equation for this surface is:

If one of the curves is replaced with a point, the equations simplify to one of:

A ruled face with no curves and two points is degenerate and will not be returned.

HermiteFace

A cubic Hermite spline face. The Revit API provides:

• Arrays of the u and v parameters for the spline interpolation points.
• An array of the 3D points at each node (the array is organized in increasing u, then increasing v).
• An array of the tangent vectors at each node.
• An array of the twist vectors at each node.

The parametric representation of this surface between nodes (u1, v1) and (u2, v2) is:

Here, U = [u³ u² u 1]^T, V = [v³ v² v 1]^T, and M_H is the Hermite matrix:

B is the coefficient matrix obtained from the face properties at the interpolation points:

Face analysis and processing

Several Face member methods provide tools suitable for use in geometric analysis:

• Intersect: computes the intersection between the face and a curve.
• Project: projects a point on the input face, and returns information on the projection point, the distance to the face, and the nearest edge to the projection point.
• Triangulate: returns a triangular mesh approximating the face. Similar to Curve.Tessellate, this mesh's points are accurate within the input tolerance used by Revit (slightly larger than 1/16').

The Intersect method can be used in to identify:

• The intersection point(s) between the two objects.
• The edge nearest the intersection point, if there is an edge close to this location.
• Curves totally coincident with a face.
• Curves and faces which do not intersect.

The next instalment of this series will look at face edges and their directions and parametrisation.